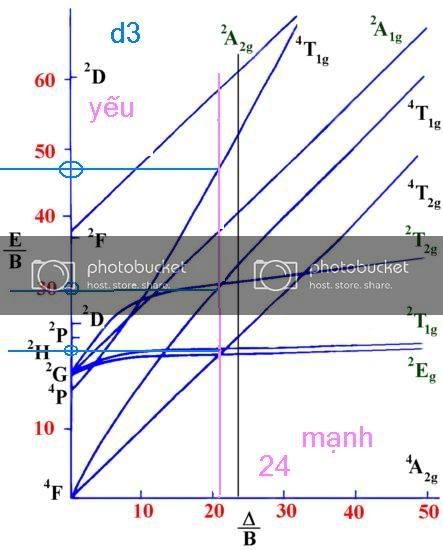
Đồ thị Tanabe –Sugano (TS). An alternative method is to use Tanabe Sugano diagrams, which are able to predict the transition energies for both spin-allowed and spin-forbidden transitions, as well as for both strong field (low spin), and weak field (high spin) complexes.
Như vậy nó cho phépxác định số chuyển mức nặng lượng, tính bứơc sóng của năng lượng ứng với các chuyển mức đó.Chứ không cho phép xác định trực tiếp cấu trúc của fức. thành thật xin lỗi hìhì. Vài điểm chú ý: Ở đây là giản đồ trong trường bát diện. Năng lượngcảu các số hạng của các ion tự do là 1hàm thông qua thông số racah A, B, C Thông số Racah là những thông số để chỉ tương tác giữa các e ở phân lớp d. Và khi đạt Ion kim loại tự do trong 1 trường fối tử nào đó thì lại trên trời rơi xuống 1 tham số nữa là thông số dt:) thông số tách. Chính vì vậy tòan bộ năng lượng của từng số hạng là một hàm số của 4 ẩn số. E = f(A,B,C,dt:) ) là 1 điều mà 2 ông đầu hàng. Chính vì thế bằng bán kinh nghiệm 2 ông rút ngắn còn hai thông số B và dt:) . và từ đó dựng lên giãn đồ dưới đây.
Biểu diễn E/B = f (dt:) / B )
Giá trị dt:) / B là trục hoằnh. mỗi giãn đồ có 1 mốc là ranh giới của trường yếu và trường mạnh.
Bên phải là trường mạnh, bên tay trái là trường yếu.
Năng lượng cơ bản được xem là mức gốc (tung độ là O ).
Chú ý từ đồ thị Tanabe–Sugano của các cấu hình d 4-5-6-7 các đường biểu diễn năng lượng của các số hạng có điểm gẫy, đấy là ranh giới chuyển từ trường yếu sang trường mạnh . ranh giới này được biểu thị bởi 1 đường thẳng song song với trục tung, đi qua điểm có hoằnh độ ứng với sự chuyển số hạng cơ bản của hệ. Còn với cấu hình d1-2-3-8-9 không có sự phân biệt trường yếu hay trường mạnh, vì sự sắp xếp các e và các mức năng lượng là không phụ thuộc vào từng số hạng năng luợng.
Ví dụ: Mang tính lý thuyết. Xét phức Cr(NH3)6 +3 , phối tử NH3 có dt:) = 21550 cm-1 . và Cr3+ B = 1030 cm-1 Yêu cầu đính dự đóan số sóng của bức xạ bị hấp thụ, và xác định các bước sóng đó.
Trước hết dựa vào giãn đồ Tanabe- Sugano của Cr3+ (d3 ) ta biết số hạng cơ bản là 4A2g với độ bội spin là 2*(3/2) +1 = 4.
Ta xác định tỷ số dt:) / B=21550 : 1030 = 20.92 ( < 24 ) hay 1 số tài liệu kí hiệu Dp thay cho dt:) với Dp*10 = dt:).
Vậy phức trên thuộc vào trường yếu tức cấu hình t32g tuy nhiên cấu hình d3 ko phụ thuộc trường mạnh hay trường yếu.
Tiếp theo vẽ 1 đường thẳng song song trục tung từ điểmcó hoằnh độ là 20.92. Áp dụng quy tắc chọn lọc (selection rule), thì các chuyển mức cho phép sẽ là
4A2g -----> 4T2g (1) hcf1 = E(4T2g) – E (4A2g) # dt:) trong trường bát diện
4A2g -----> 4T1g (F) (2) hcf2= E(4T1 F ) – E (4A2g)
4A2g -----> 4T1g (P) (3) hcf3 = E(4T2g P) – E (4A2g)
Ví dụ 2 : Dự đóan các đạc trưng cảu phổ hấp thụ e của các phức chất sau và so sánh giữa chúng [Fe(en)3]2+ và Fe(CN)6 4- , biết dt:) của cá phối tử lần lượt là en = 12.000cm-1 và CN- = 32.200 cm-1 (Trong trường bát diện , và B (Fe2+) = 1058)
Trả lời. Nếu phối tử là en có dt:) / B = 11,34 < . Còn phối tử là CN- dt:) /B = 31,43 . Như vậy phức [Fe(CN)6 ]2- là phức trường mạnh với số hạng cơ bản là 1A1g với các chuyển mức có thể xảy ra theo quy tắc chọn lọc .
1A1g – > 1T1g
1A1g – > 1T2g
1A1g – > 1Eg
1A1g – > 1A2g
1A1g – > 1A1g
Vậy trên phổ UV có thể có 5 pic (lý thuyết) nhưng chắc chắn nhiều hơn 2.
Còn phức [Fe(en)3 ]2+ với số hạng cơ bản 5T2g cấu hình e (t42g ,e2g) thì chỉ có 1 chuyển mức khả quy là 5T2g –> 5Eg vì vậy chỉ có 1 píc duy nhất.
Hình
Tuy nhiên thường trong thực theo atbu được biết thì thường người ta làm chuyện ngược lại tức biết được vị trí các pic sau đó xác định thông số racah B và thông số tách dt:). Vídụ 3. như bài tập http://www.cbu.edu/~mcondren/c422e305.htm
Việc xác định cấu trúc của phức bát diện hay tứ diện thì phức tạp hơn. Trong các tài liệu hầu hết là đưa giả đồ Tanabe- Sugano của ion trong trường bát diện , còn trong trường tứ diện thì sao?!! Khi ấy người ta áp dụng thêm giản đồ Orgel và hiệu ứng không cắt nhau của các số hạng đồng dạng (noncrossing rule ). Và sử dụng phương pháp ngọai suy giả sử từng cấu trúc xem lý giải cái nào phù hợp. Tuy nhiên mìhn là người ko chuyên về mảng này nên chỉ biết thế hix, chưa tìm hiểu nhiều. bác nào biết thì giới thiệu thêm cho anh em. :art (